Global Interval Timer

This item relates to the broader goal of modeling object behaviors in Monty.

We want to have an interval timer that exists separately from the current Monty components and provides input to a large group of LMs (or all).

The interval timer is a bit like a stop watch that counts up time from a previous event and broadcasts this elapsed time widely. The time can be reset by significant events that are detected in LMs (or SMs).

In the brain, this elapsed time might be encoded with time cells (e.g. see Kraus, 2013) or a similar mechanism, where different cells fire at different temporal delays from the start of an interval. Together they tile the temporal space (up to a certain max duration and with higher resolution for shorter durations). This means that the LM receives different neural input from the timer, depending on how much time has passed since the start of this state.

In the conceptual figure below, this mechanism is illustrated as the circle with little purple dots on it. Each significant event resets the circle to have the top neuron (darkest purple) active. Then, as time passes, the neurons on the circle become active in a clockwise direction. The ID of the active time neuron is the input to L1 of the cortical column.

There is a default speed at which the timer goes through the different active states. This is the timing information stored during learning. During inference, however, the column can tell the interval timer to spin faster or slower, which means that it will receive the same neural input to L1 at different absolute times from the last event. Note that there is no continuous "time-since" signal but instead there are discrete representations for different elapsed intervals and hence, these representations can change faster or slower and be associated with features in the models.

Example 1: A Melody (no location representation needed)

The animation below shows an example of learning a melody. Here, each note is a significant event that resets the timer.

Whatever an input feature (here, the note, although one could also use a background beat instead) comes into the column/LM, it gets associated with the L1 input that is received at the time, which represents the time passed since the last event.

Whenever the timer is reset, we move forward by 1 in the element in the sequence (here mapped onto L5b, but that is speculative. Since we only move through the sequence in one direction, no path integration is needed.)

In the continuation of this example below you can see that if there is a longer interval, the clock will spin further through the different neural representations and the next feature will be associated with a later on (lighter purple).

Example 2: A Behavior

Next, let's look at an example of an object behavior. Here we have both discrete events (when the stapler starts moving and when it reaches it’s lowest position and staples) and continuous changes between events. This could be using the above mechanism as follows:

The clock is reset and starts ticking through the different neural activations as before. However, as we activate different time cells, we receive different inputs in L4 and associate these different inputs with the different time cells. This allows us to represent feature inputs at different offsets after the last significant event. When a significant event occurs (i.e. stapler reaches the bottom position and tacks some paper), the clock is reset and we move one forward in the element in the sequence (L5b)

One other change here is that we are sensing in 3D space (2D in the example diagram), so in addition to our position in the sequence, we have a location on the object (L6a, shown as grid here). This location is updated using sensor movement (our existing mechanism). In the example here, the sensor doesn’t move so we just store sequence information at that location but if we explore a behavior over and over again at different locations, this would become a richer representation of the entire object behavior.

The learned model would then look as shown below. We have discrete states in a sequence (movement through the sequence is determined by resets of the global clock). Each state can store features at different locations at different intervals after the last event (colored arrows).

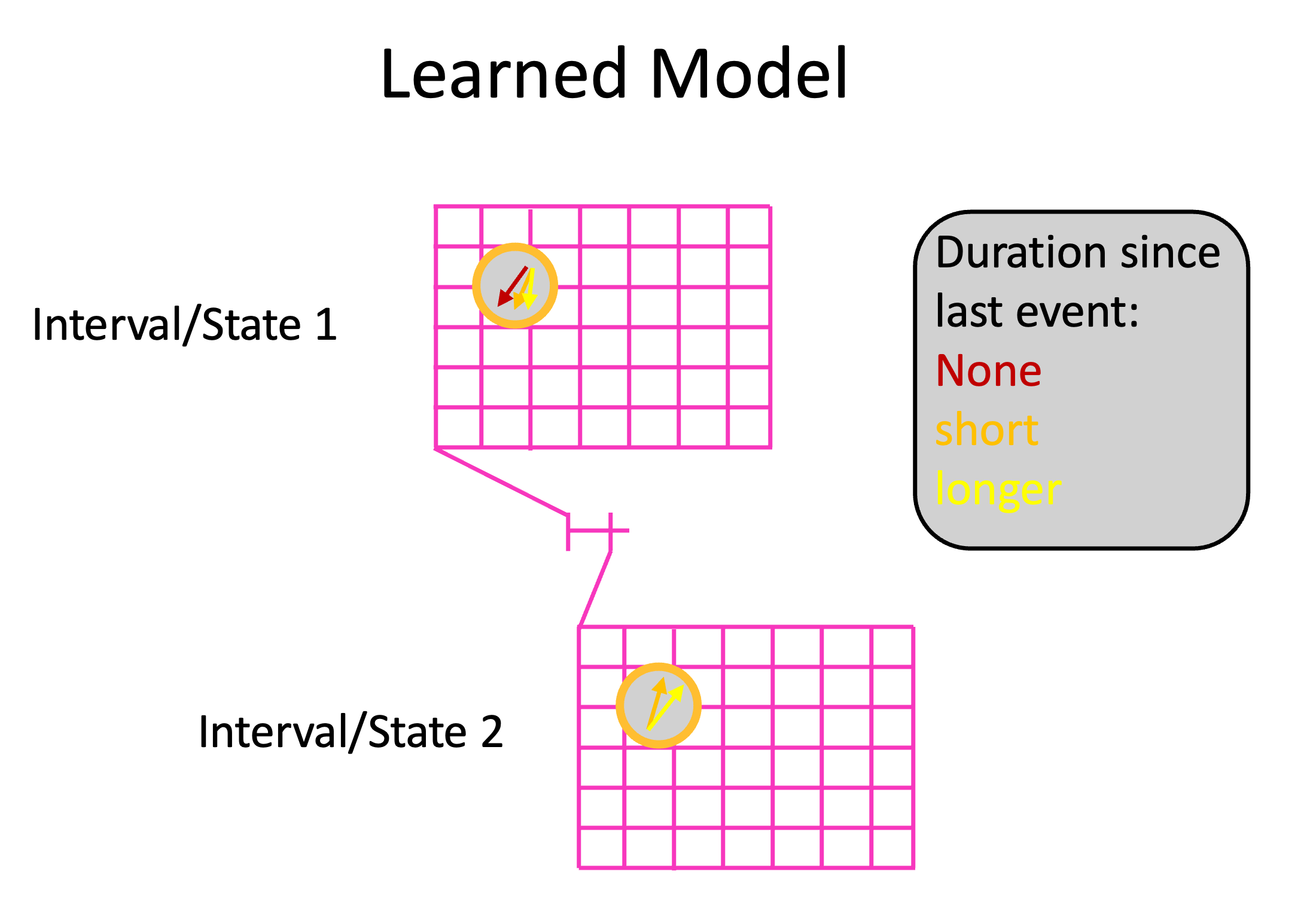
Learned behavior model. For each state Monty stored different features at different locations. Additionally, within a state, different features can be associated with different temporal offsets since the beginning of the interval.

For inference, we would need to infer the location in the object’s reference frame, as usual. In addition, we need to infer the location in the sequence (in the sequence of discrete states). The interval within each state does not need to be inferred, as it is provided by the global clock. (see page on including state in hypotheses)

However, if there is a mismatch between which feature is sensed and the expected feature based on the input into L1, this can be used as a signal to speed up or slow down the global clock (see page on speed detection to adjust timer).

Higher resolution and lower matching tolerance for short durations compared to long ones could be implemented by tiling the short duration more densely (i.e. having more distinct neural representations as input to the LM for those).

Help Us Make This Page Better

All our docs are open-source. If something is wrong or unclear, submit a PR to fix it!

Make a Contribution

Learn how to contribute to our docs