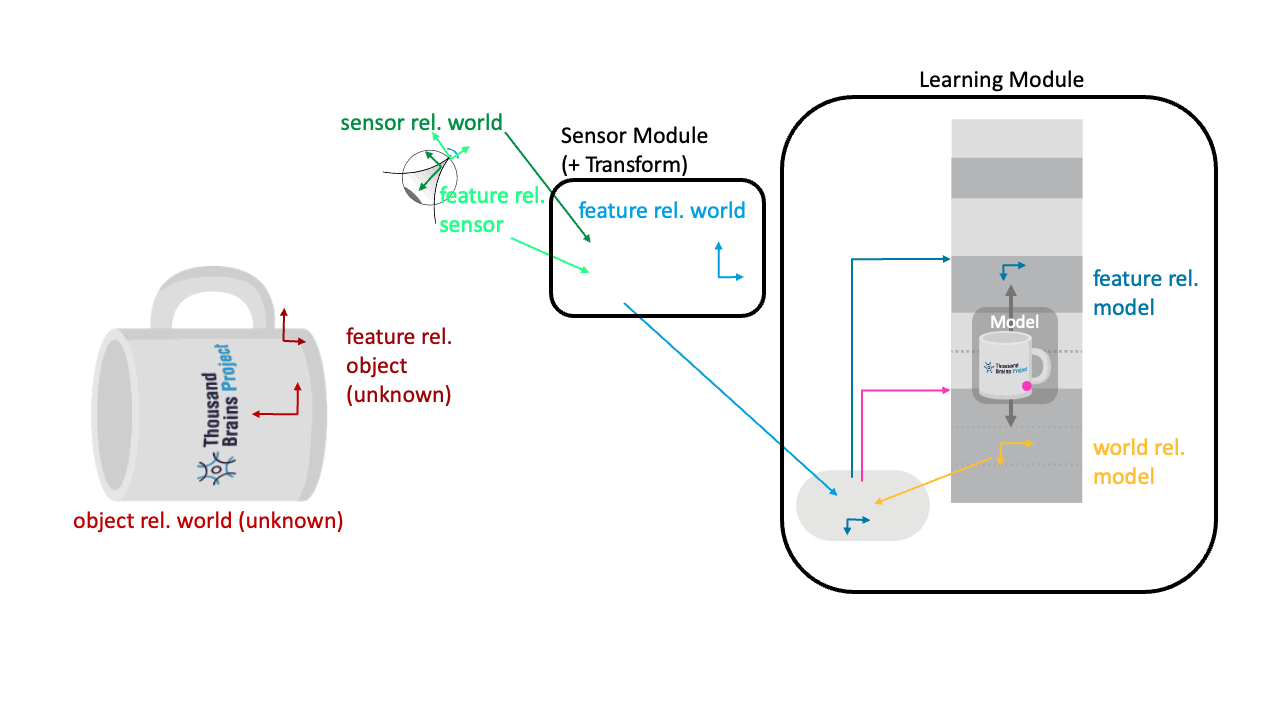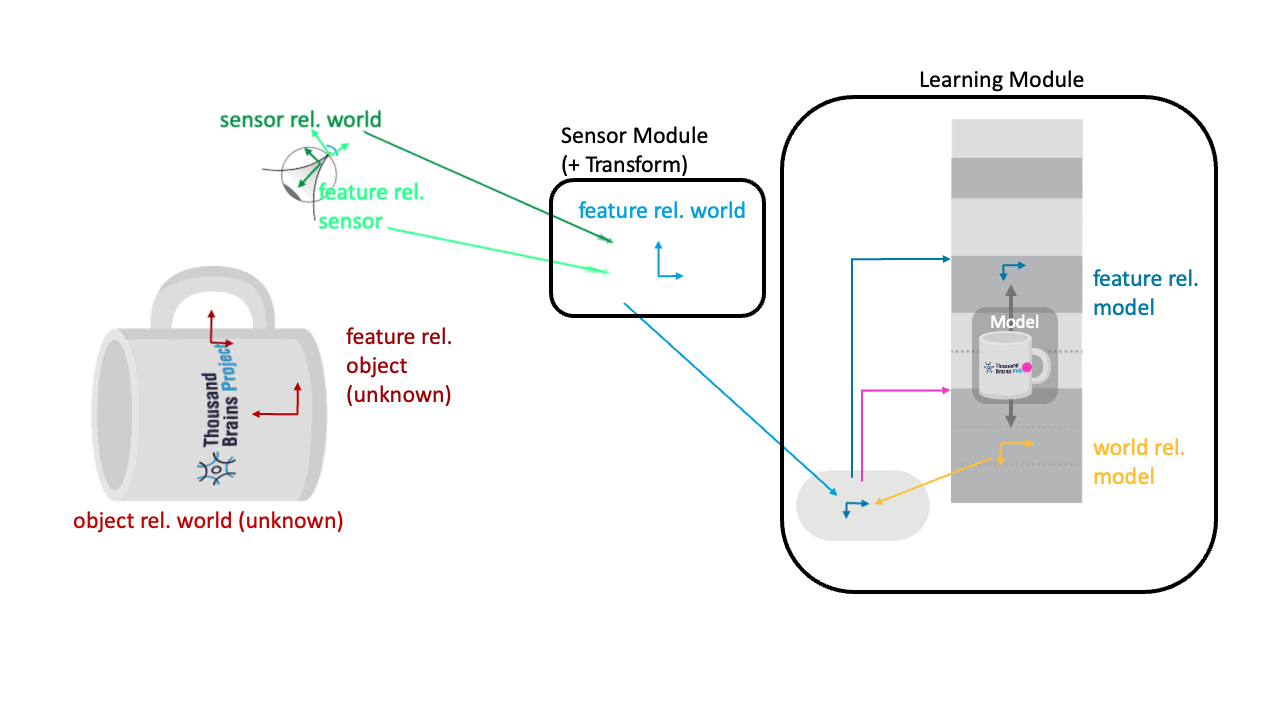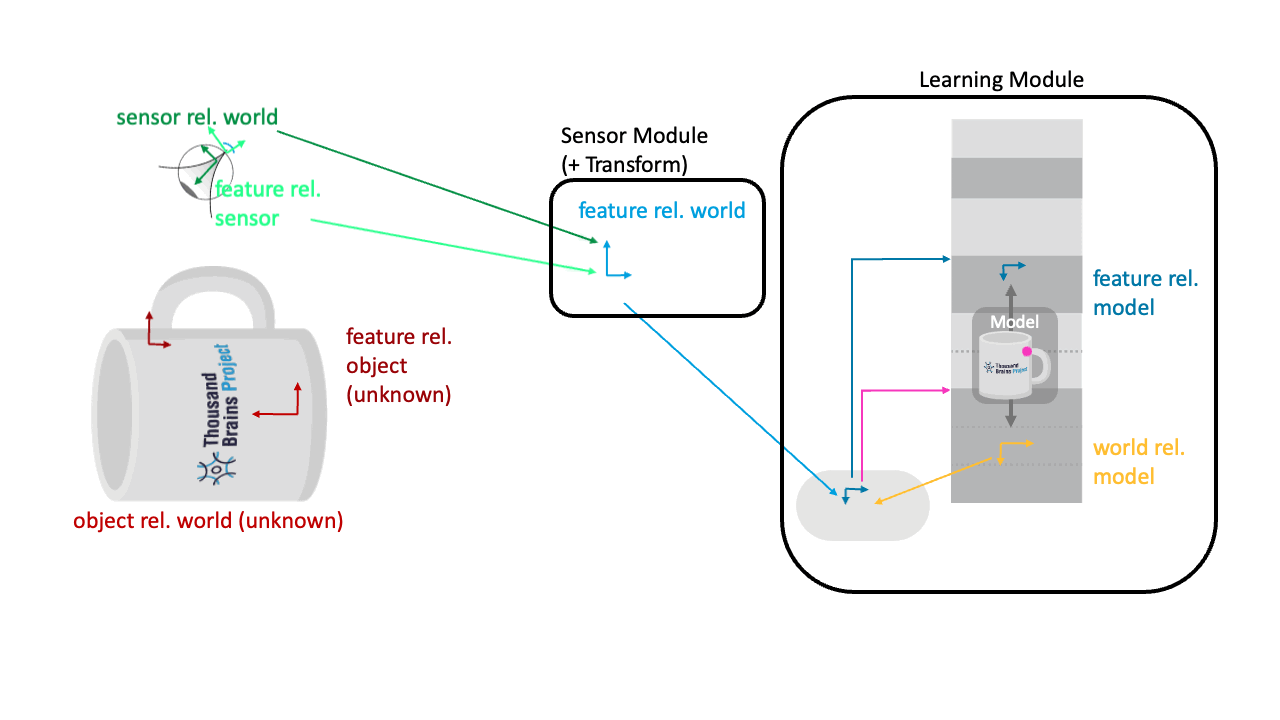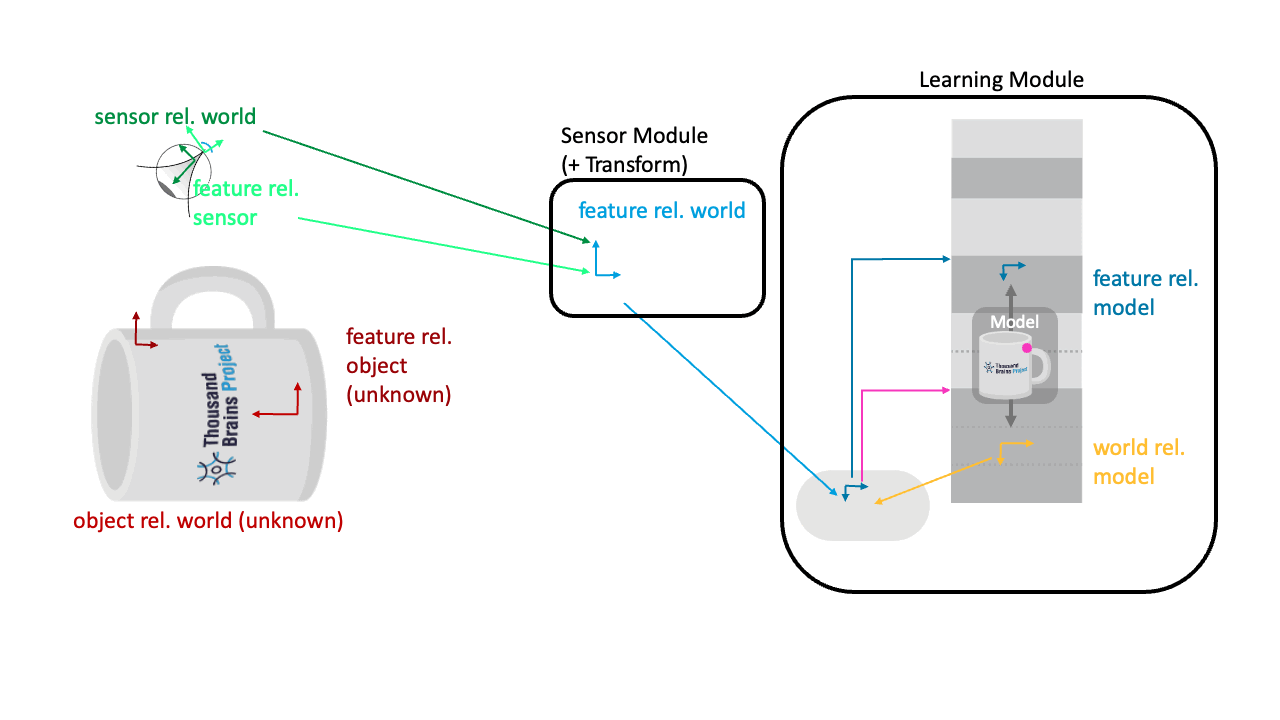
Reference Frame Transforms
In a sensorimotor learning setup, one naturally encounters several different reference frames in which information can be represented. Additionally, Monty has internal reference frames in which it learns models of objects. Those can get confusing to wrap your head around and keep track of, so here is a brief overview of all the reference frames involved in a typical Monty setup.
Reference Frames in a Typical Monty Experiment
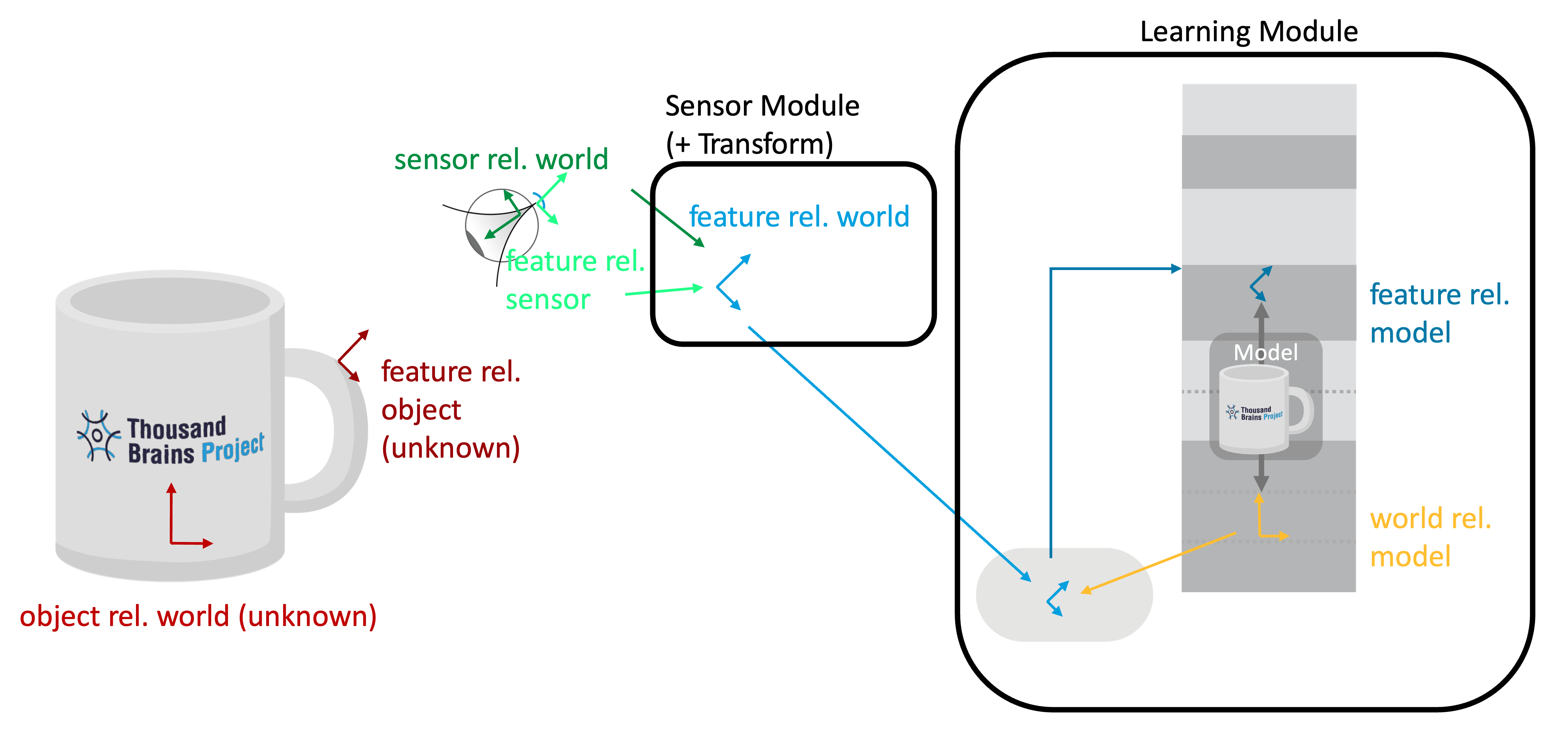
🔴 Object rel. World
The orientation of the object in the world (unknown to Monty). For instance, if we use a simulator, this would be the configuration that specifies where the object is placed in the environment (like we do here). In the real world we don't have a specific origin, but all objects are still in a common reference frame with relative displacements between each other.
🔴⚫️ Feature rel. Object
The pose of all the features on the object (also unknown to the Monty). For instance, if you use a 3D simulator, this could be defined in the object meshes.
🟢⚫️ Sensor rel. World/Body
The sensor’s location and orientation in the world can be estimated from proprioceptive information and motor efference copies. Basically, as the system moves its sensors, it can use this information to update the locations of those sensors in a common reference frame. For the purposes of Monty it doesn't matter where the origin of this RF is (it could be the agent's body or an arbitrary location in the environment) but it matters that all sensor locations are represented in this common RF. In simulation environments, this pose estimation can be perfect / error-free if desired, while in the real world you usually have noisy estimates.
🟢⚪️ Feature rel. Sensor
This is the feature's orientation relative to the sensor. For instance in Monty, we often use the surface normal and curvature direction to define the sensed pose, which are extracted from the depth image of the sensor (code).
🔵 Feature rel. World/Body
The estimated orientation of the sensed feature in the world (sensor_rel_world * feature_rel_sensor). In Monty, this currently happens to the depth values in DepthTo3DLocations while the surface normal and curvature extraction then happens in the SM, but in the end you get the same results.
🟡 World rel. Model
This is the hypothesized orientation of the learned model. It expressed how the incoming features and movements need to be transformed to be in the model's reference frame. This orientation needs to be inferred by the LM based on its sensory inputs. There are usually multiple hypotheses which Monty learning modules keeps track of in self.possible_poses
The inverse of this pose (model rel. world) expresses how the model would need to be rotated to overlay correctly onto the object in the world. We use this inverse as Monty's pose classification to calculate it's rotation error.
🔵⚫️ Feature rel. Model
This is the rotation of the currently sensed feature relative to the object model in the LM (feature_rel_world * object_rel_model, see code here). The learning module uses its pose hypothesis to transform the feature relative to the world into its object's reference frame so that it can recognize the object in any orientation and location in the world, independent of where it was learned.
For a description of these transforms in mathematical notation, see our pre-print Thousand-Brains Systems: Sensorimotor Intelligence for Rapid, Robust Learning and Inference.
In the brain we hypothesize that the transformation of sensory input into the object's reference frame is done by the thalamus (see our neuroscience theory paper for more details).
Keeping Input to the LM Constant as the Sensor Moves
The transform in the sensor module combines the sensor pose in the world with the sensed pose of the features relative to the sensor. This way, if the sensor moves while fixating on a point on the object, that feature pose will not change (see animation below). We are sending the same location and orientation of the feature in the world to the LM, no matter from which angle the sensor is "looking" at it.
This is one of the key definitions of the CMP: The pose sent out from all SMs is in a common reference frame. In Monty, we use the DepthTo3DLocations transform for this calculation and report locations and orientations in an (arbitrary) world reference frame.
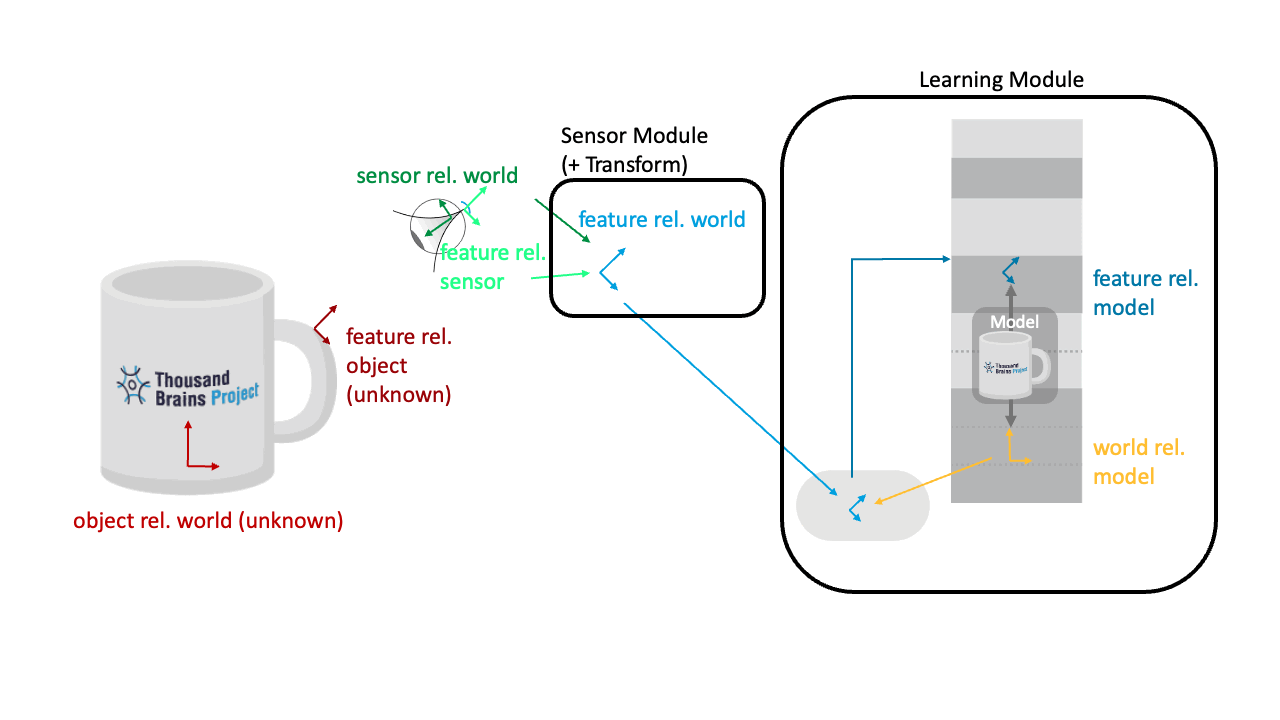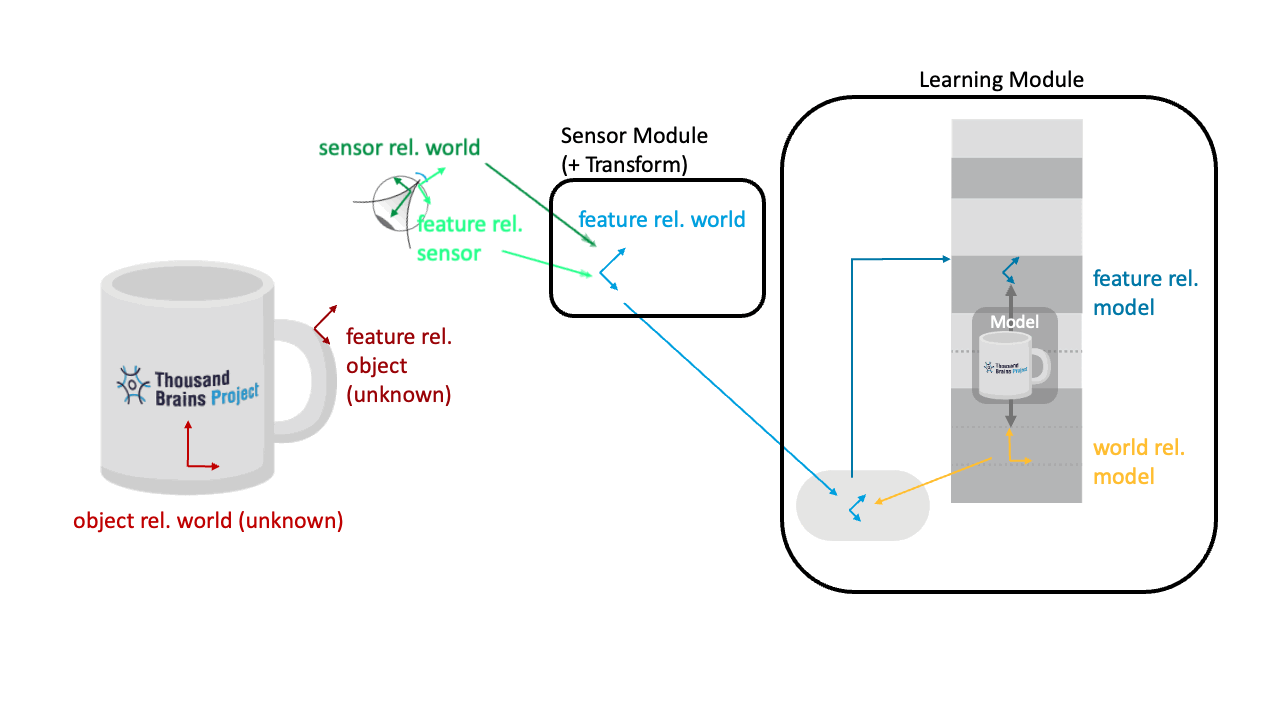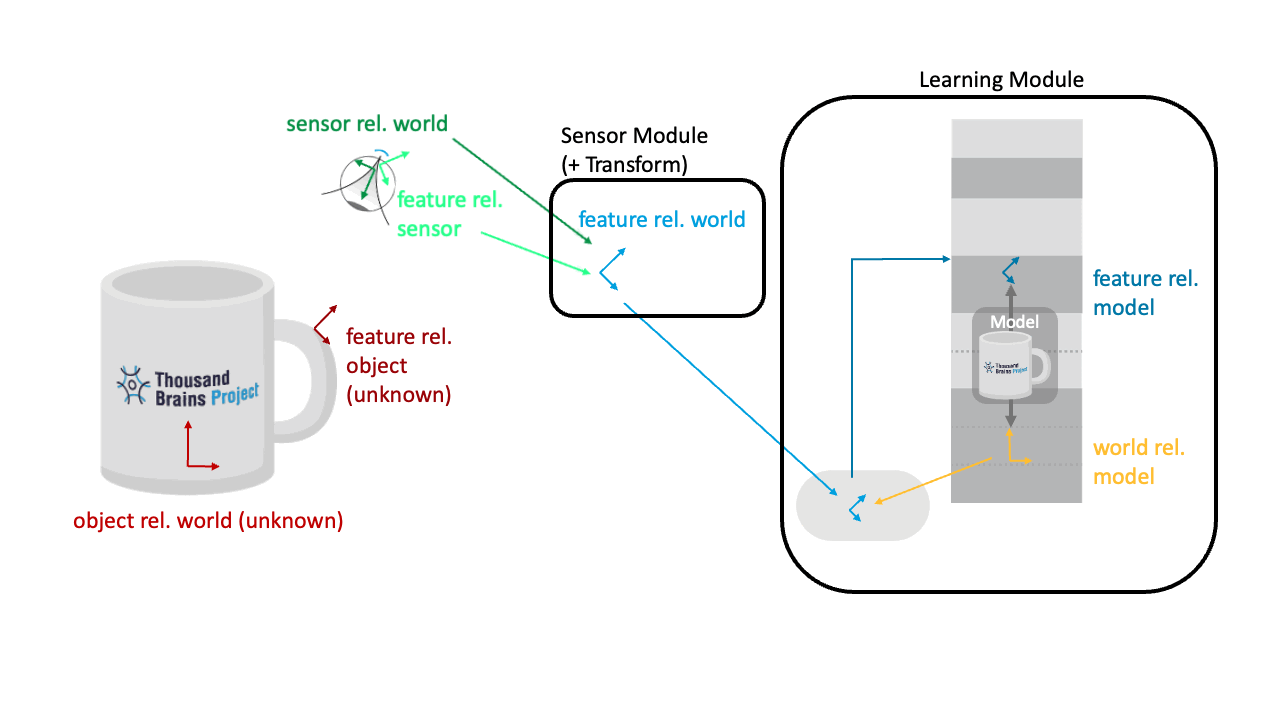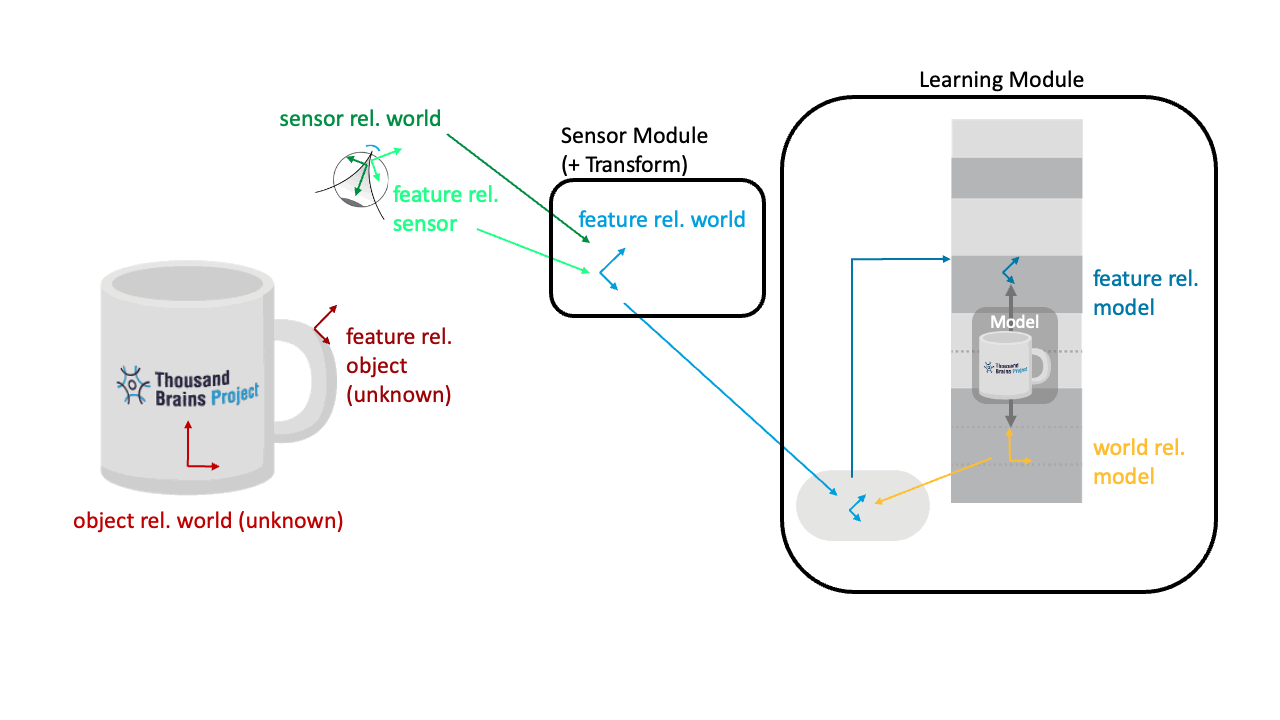
Applying the Pose Hypothesis as the Object Rotates
If the object changes its pose in the world, the pose hypothesis in the LM comes into play. The LM has a hypothesis on how the object is rotated in the world relative to its model of the object. This is essentially the rotation that needs to be applied to rotate the incoming features and movements into the model’s reference frame.
If the object is in a different rotation than how it was learned, all the features on the object will be sensed in different orientations and location in the world. This needs to be compensated by the yellow projection of the pose hypothesis. This way, the incoming features used for recognition (dark blue) remain constant as the object rotates.
The plot below only shows one pose hypothesis, but in practice, Monty has many of them, and it needs to infer this pose from what it is sensing (dark green orientations are unknown). The animation also assumes that Monty is correctly inferring and updating it's hypothesis as the object is rotating in the world, which is not trivial.
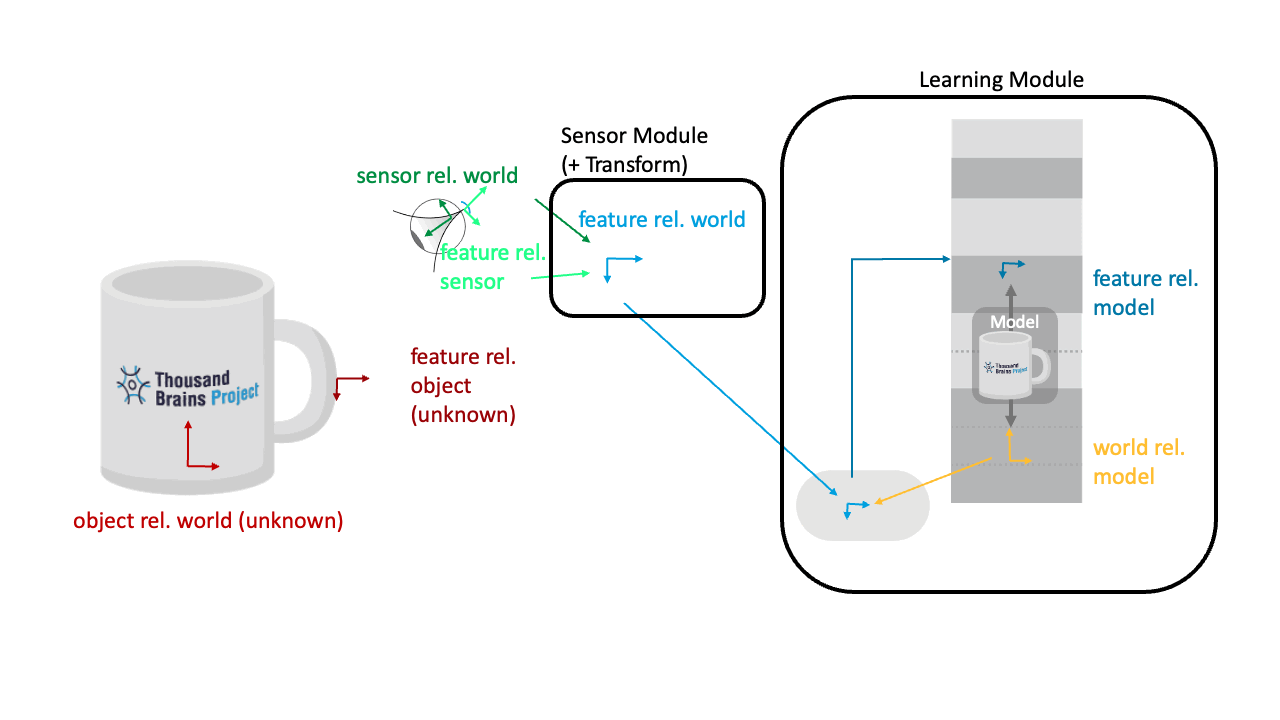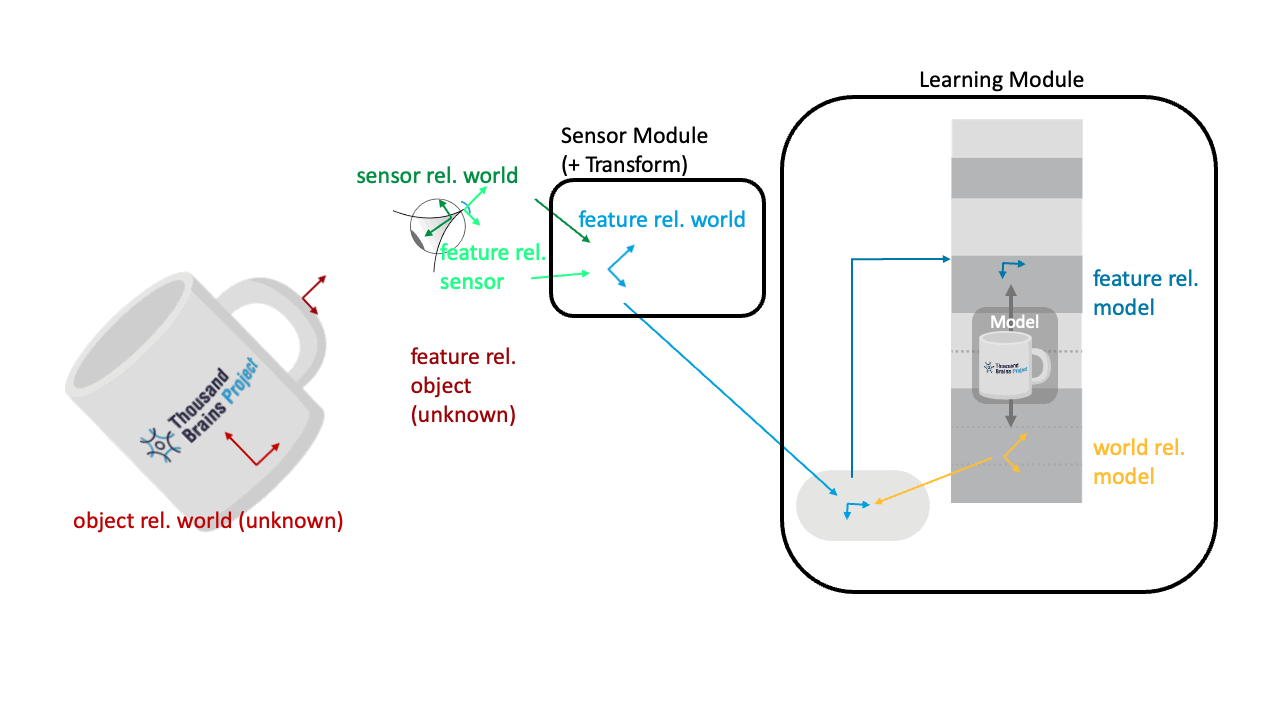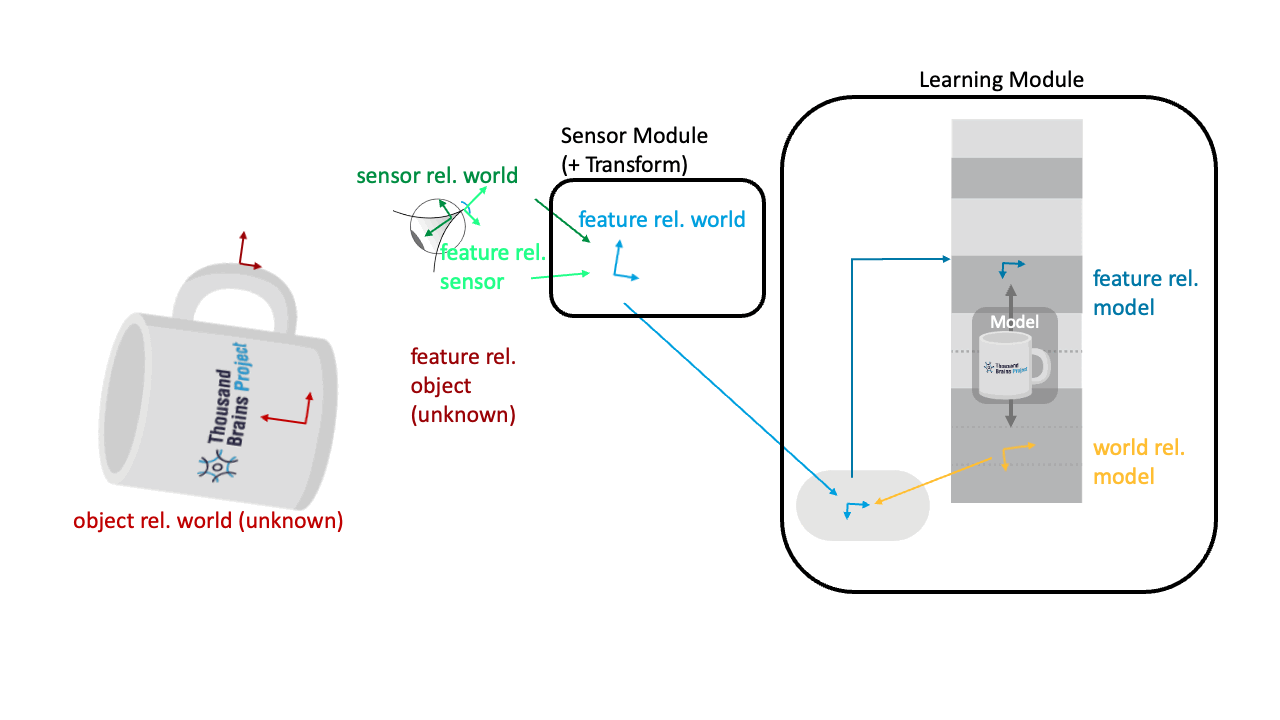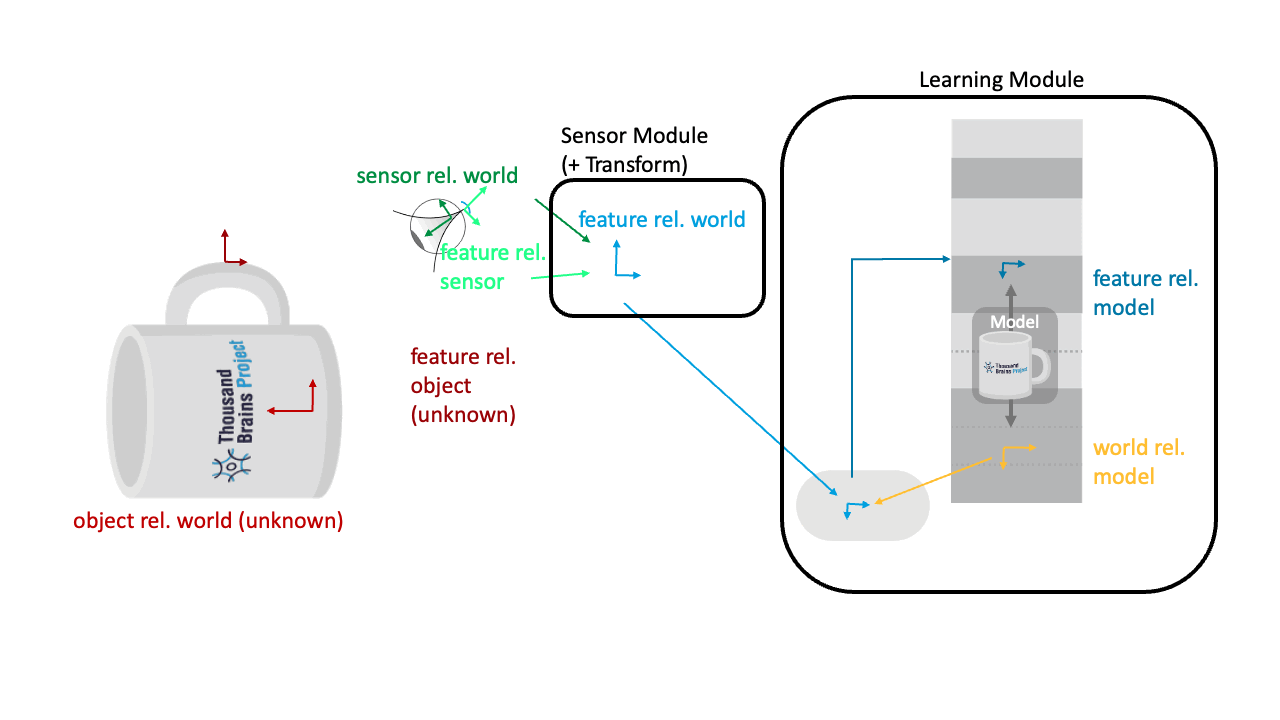
Applying the Pose Hypothesis to the Sensor Movement
What is not shown in the visualizations above is that the same rotation transform is also applied to the movement vector (displacement) of the sensor (pink). In Monty we calculate how much the sensor has moved in the world by taking the difference between two successive location and orientation inputs to the LM (code). The sensor movement is applied to update the hypothesized location on the object (pink dot).
Before we can apply the movement to update our hypothesized location on the object, the movement needs to be transformed from a movement in the world to movement in the object's reference frame. To do this, the hypothesized object orientation (yellow) is applied, the same way it is applied to the incoming features.
So for example, if object is rotated by 90 degrees to the left and the sensor moved right to left on the object (like in the animation shown below), then the orientation transform will update the location on the object model (pink dot) to move from bottom to top of the object.
Applying the hypothesized object rotation to both the incoming movement and features means that Monty can recognize the object in any new location and orientation in the world.
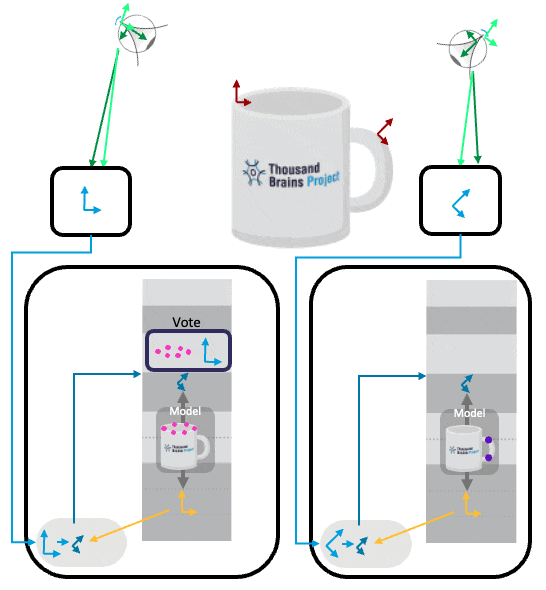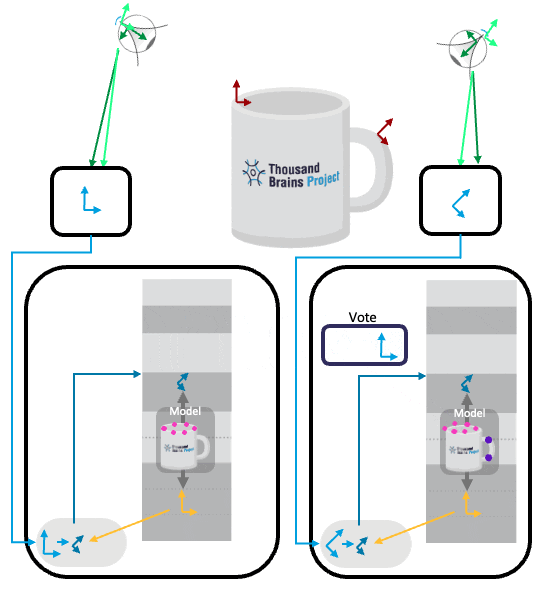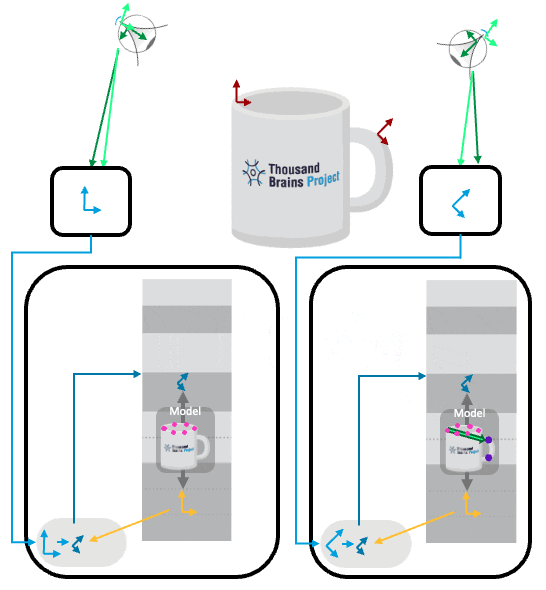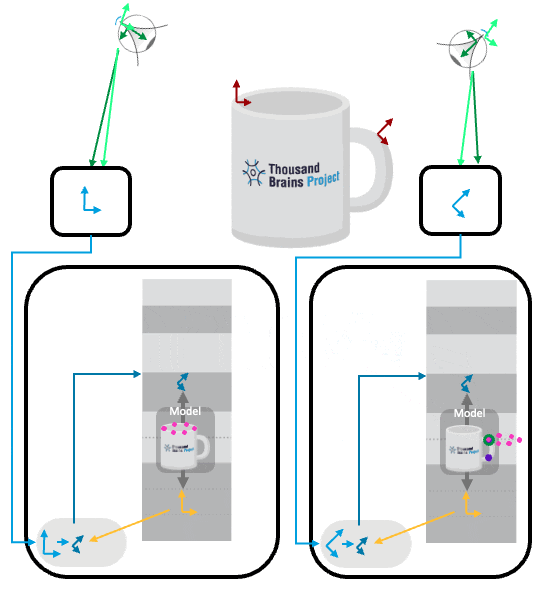
Reference Frame Transforms for Voting
Voting in Monty happens in model space. We directly translate between the model's RF of the sending LM to the model's RF of the receiving LM. This relies on the assumption that both LMs learned the object at the same time, and hence their reference frames line up in orientation and displacement (since we receive features rel. world, which will automatically line up if the LMs learn the object at the same time). Otherwise, we could store one displacement between their reference frames and apply that as well.
The two LMs receive input from two sensors that sense different locations and orientations in space. They receive that as a pose in a common coordinate system (rel. world in the image below). Since the sensors are at different locations on the object and our hypotheses are “locations of sensor rel. model” we can’t just vote on the hypotheses directly, but have to account for the relative sensor displacement. For example, the sensor that is sensing the handle of the cup needs to incorporate the offset to the sensor that senses the rim to be able to use its hypotheses.
This offset can be easily calculated from the difference of the two LM’s inputs, as those poses are in a common coordinate system. The sending LM attaches its sensed pose in the world to the vote message it sends out (along with its hypotheses about the locations on the mug), and the receiving LM compares it with its own sensed pose(green arrow) and applies the displacement to the vote hypotheses (shifting the pink dots).
Check out our evidence LM documentation for more details on voting.
Example: Both Sensors Sense Same Location
The simplest example is if both learning modules receive input from the same location in the world (i.e. the two sensors "look" at the same point). In this case, no transformation needs to be applied to the incoming votes (no transformation is represented as a green dot in the figure) and they can directly be overlaid onto the receiving LM's reference frame.
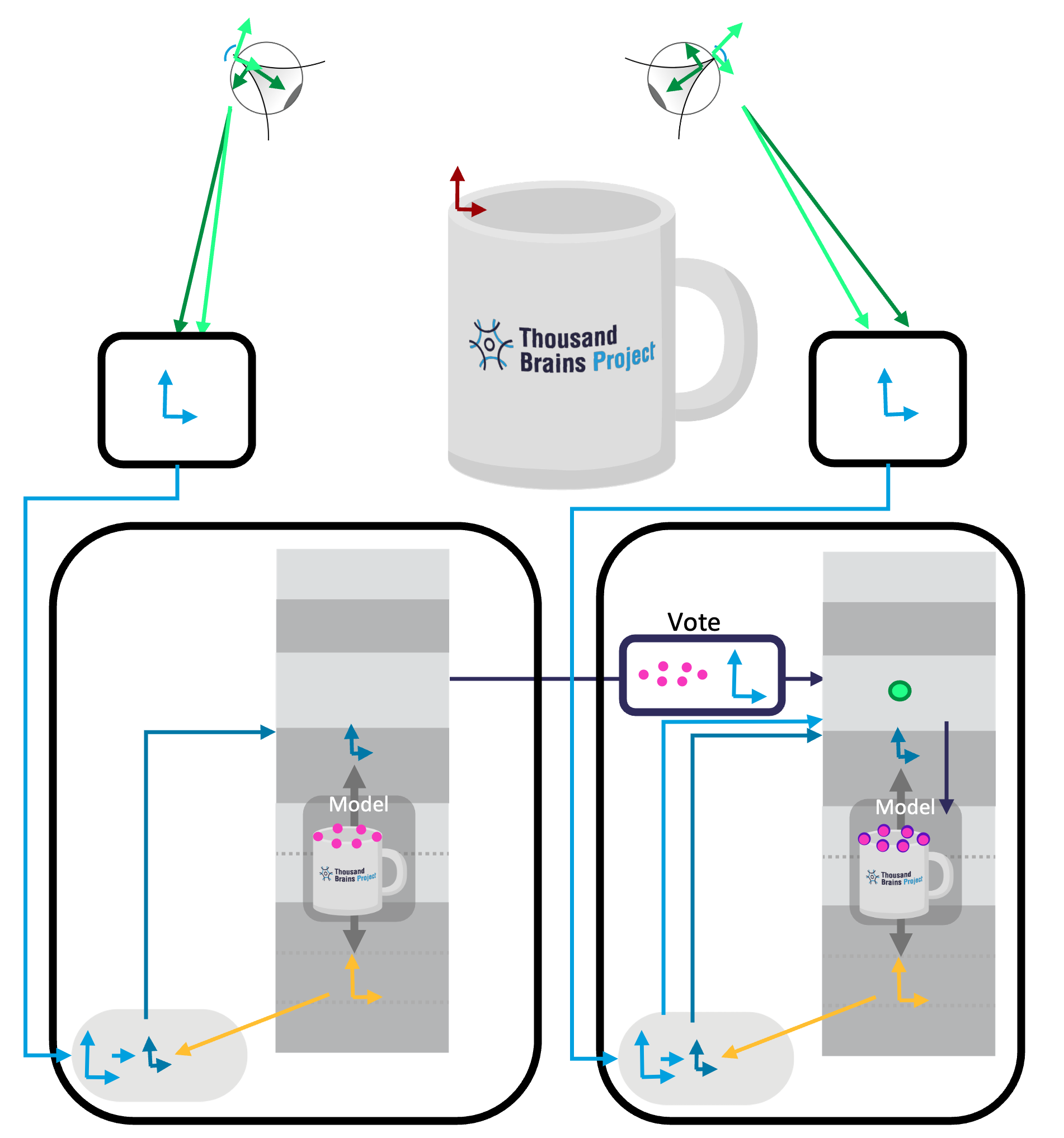
However, voting in this case does not help reduce ambiguity as both LMs receive the same input.
Example: Sensors Sense Different Locations
If the two LMs receive input from two different locations in the world (like in the animation above and the image below), we need to calculate the displacement between the two and apply it to the incoming votes. In the example below, the left LM is sensing the left side of the rim and the right LM is sensing the handle. When the right LM receives votes from the left one, it needs to shift those down and towards the right. You can think of the right LM saying "if you are over there, and you think you are at this location on the mug, then I should be x amount to the lower right of that".
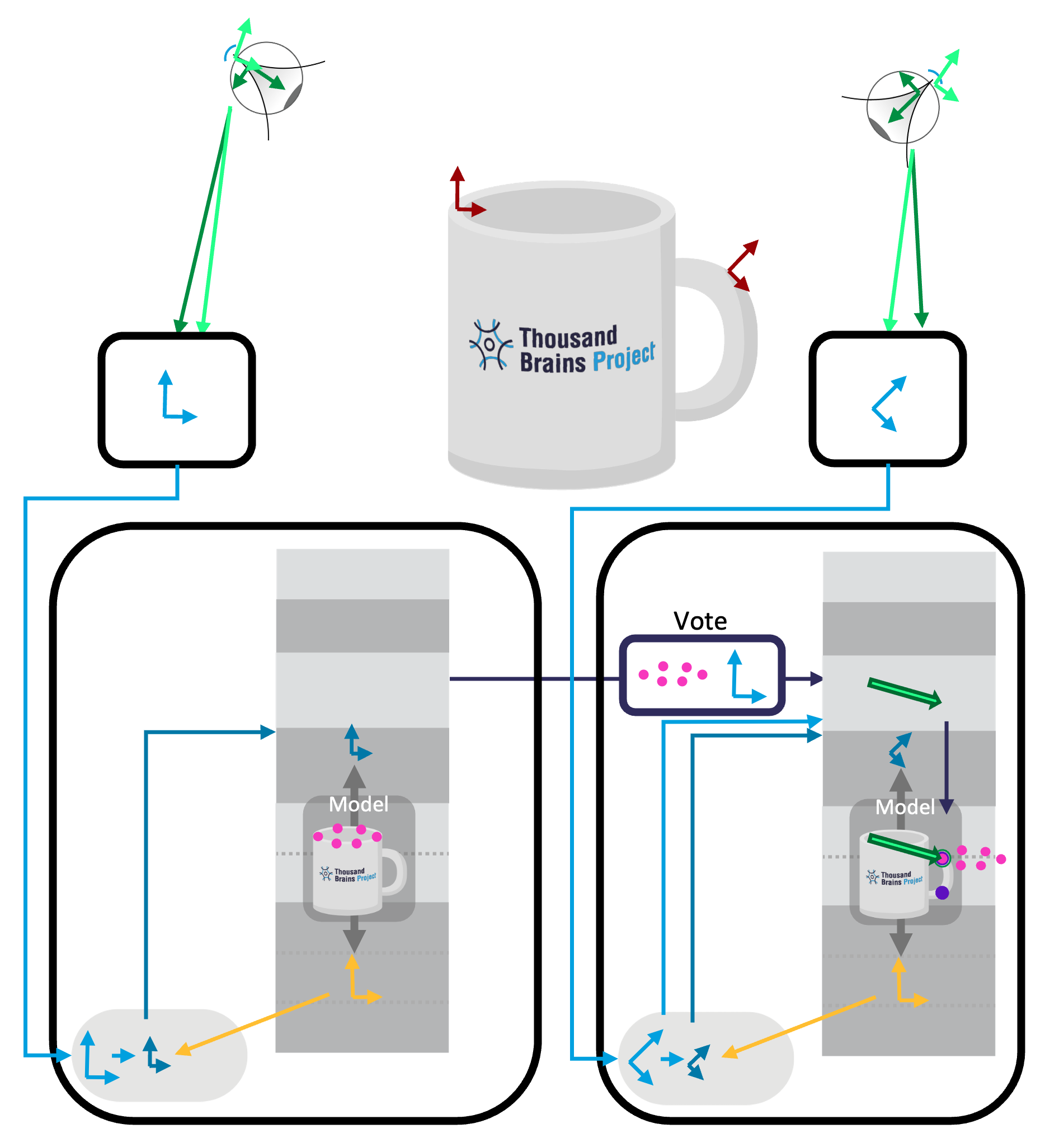
The displaced votes are overlaid onto the existing location hypotheses of the receiving LM (purple dots). Only a few points will be consistent with the incoming votes (in this case just one, circled in dark green). When the right LM sends votes to the left one, it's location hypotheses will have to be displaced in the opposite direction (towards the left).
Example: Accounting for the Pose Hypothesis
What we haven't shown so far is how voting accounts for the pose hypothesis. The examples above all illustrated cases where the object orientation in the world matched the orientation it was learned in (hence the yellow arrow did not rotate any of the input). The figures above were also simplified in that they only showed one pose hypothesis for the object. In reality, we have one pose hypothesis (yellow arrows) for each hypothesized location (pink dots).
When voting, the sending LM does not only send it's location hypotheses but also the hypothesized pose of the model, where there will be one such pose for each location hypothesis sent. The receiving LM then used these poses to rotate the sensor displacement (thick green arrow). This is similar to how sensor movement in the world needs to be rotated into the model's reference frame.
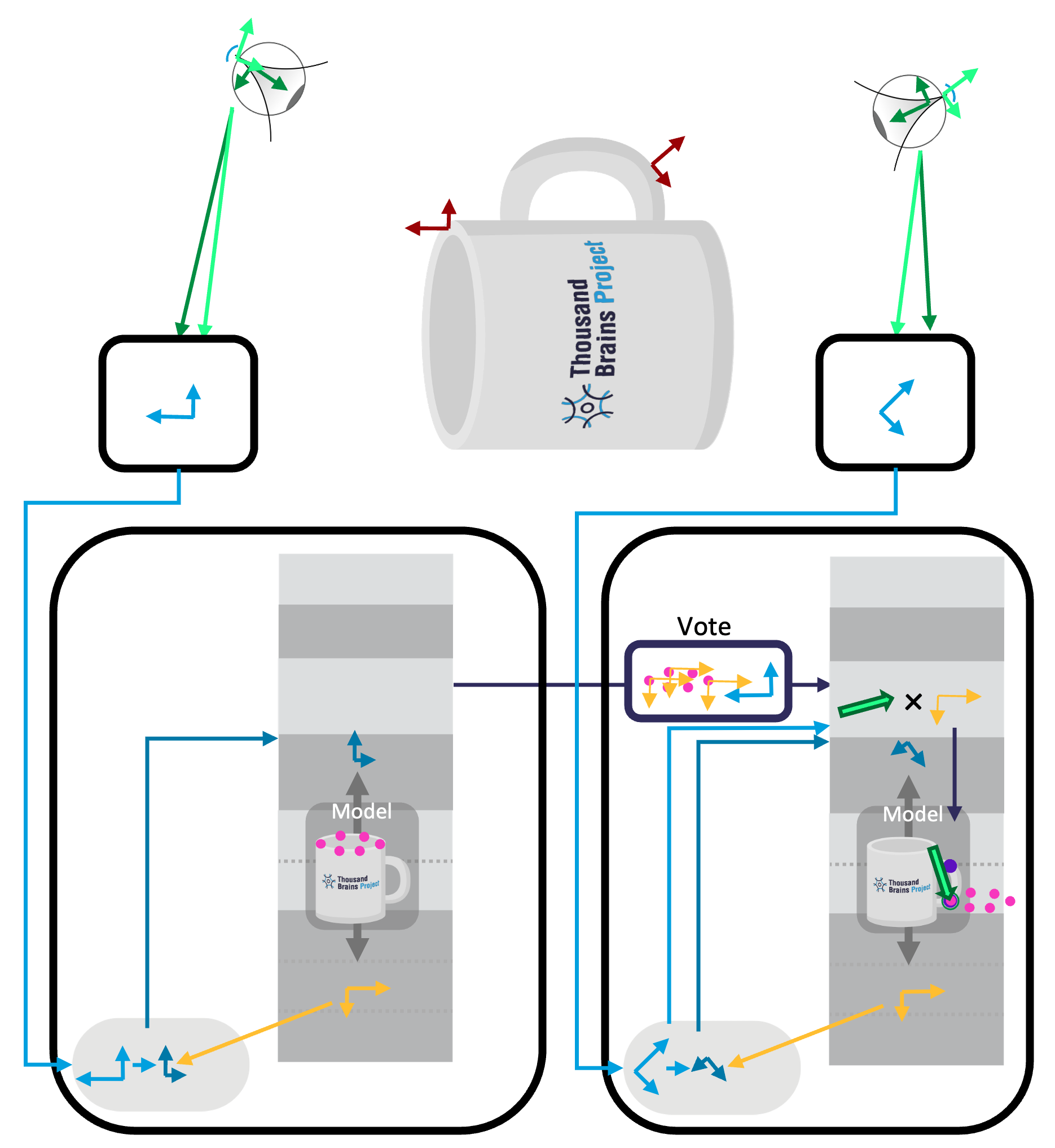
After this displacement is applied, the vote locations (pink dots) can again be overlaid onto the existing hypothesis space (purple dots).
Help Us Make This Page Better
All our docs are open-source. If something is wrong or unclear, submit a PR to fix it!
Updated about 1 hour ago
